Revit Formulas for Everyday Usage
Below is a copy of the information as provided at this RevitForum article. Formulas referenced below are commonly used when building Revit families.
Revit Formulas for Everyday Usage
Exponentiation
X raised to the power of Y = X ^ Y
E raised to an x power
E is a mathematical constant that is approximately equal to 2.7. It is an irrational number, but if truncated to 20 decimals, it would be 2.7182818284590452353.
Revit usage = exp(x)
Circles with pi π
Usage in Revit = pi()
Circumference = pi() * (Radius * 2)
Circumference = pi() * Diameter
Circle Area = pi() * Radius ^ 2
Arch Length = (Degree / 360) * 2 * pi() * Radius
Square Root
Fixed value = sqrt(999)
Parameter = sqrt(Width)
Formula= sqrt(Width + Height)
Logarithm
The logarithm of a number to a given base is the exponent to which the base must be raised in order to produce that number. For example, the logarithm of 1000 to base 10 is 3, because three factors of 10 must be multiplied to yield a thousand: 10 × 10 × 10 equals 1000 Revit usage = log(1000)
Force yes/no parameters to be checked or unchecked
Force checked = 1 < 2
Force unchecked = 1 > 2
Conditional statements
Conditional statement uses this structure:
IF (<condition>, <result-if-true>, <result-if-false>)
Supported Conditional Operators
< Less than
> Greater than
= Equal
/ Divide
AND Both statements are true
OR One of the statements is true
NOT Statement is false
Conditional statements can contain numeric values, numeric parameter names, and Yes/No parameters.
Simple IF Statement
IF (Length < 900, <true>, <false>)
Formula That Returns Strings
IF (Length < 900, “Opening too narrow”, “Opening OK”)
Using logical AND
IF ( AND (x = 1 , y = 2), <true>, <false>)
Returns <true> if both x=1 and y=2, else <false>
Using logical OR
IF ( OR ( x = 1 , y = 2 ) , <true>, <false>)
Returns <true> if either x=1 or y=2, else <false>
Nested IF statements
IF ( Length < 500 , 100 , IF ( Length < 750 , 200 , IF ( Length < 1000 , 300 , 400 ) ) )
Returns 100 if Length<500, 200 if Length<750, 300 if Length<1000 and 400 if Length>1000
IF with Yes/No condition
Length > 40
Returns checked box (<true>) if Lenght > 40
NOT with Yes/No condition
not(Viz)
Returns checked box (<true>) if Yes/No parameter "Viz" is unchecked, and returns unchecked box (<false>) if Yes/No parameter "Viz" is checked.
IF AND OR Returning the greatest of three values
Say you have these 3 length parameters, and want a fourth parameter to return the greater value/length of the 3:
Length A
Length B
Length C
Return Length (Returns the greatest of the three length parameters) Return Length = if(and(or(Length A > Length B, Length A = Length B), or(Length A > Length C, Length A = Length C)), Length A, if(and(or(Length B > Length A, Length B = Length A), or(Length B > Length C, Length B = Length C)), Length B, if(and(or(Length C > Length A, Length C = Length A), or(Length C > Length B, Length C = Length B)), Length C, 0 mm)))
Credit to: Joe Zhou for this formula!
Another option is to use an extra "Calc" parameter, which is a bit more clumsy but also way easier and more manageable for us mortals.
Calc = if(Length A > Length B, Length A, Length B)
Return Length = if(Calc > Length C, Calc, Length C)
And a third option:
Return Length = if(A > D, if(A > C, if(A > B, A, B), if(B > C, B, C)), if(B > D, if(B > C, B, C), if(C > D, C, D)))
Credit to: Ekkonap who posted this on May 23rd 2011.
Trigonometry for right triangles:
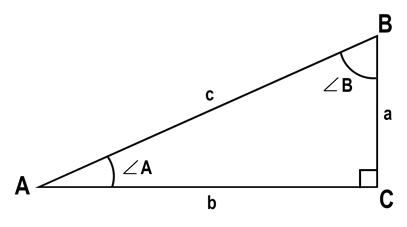
Known: a+b
c = sqrt(a ^ 2 + b ^ 2) A = atan(a / b) B = atan(b / a)
Known: a+c
b = sqrt(c ^ 2 - a ^ 2) A = asin(a / c) B = acos(a / c)
Known: b+c
a = sqrt(c ^ 2 - b ^ 2) A = acos(b / c) B = asin(b / c)
Known: c + A
a = c * sin(A) b = c * cos(A) B = 90° - A
Known: c + B
a = c * cos(B) b = c * sin(B) A = 90° - B
Known: a + B
b = a * tan(B) c = a / cos(B) A = 90° - B
Known: b + A
a = b * tan(A) c = b / cos(A) B = 90° - A
Known: a + A
b = a / tan(A) c = a / sin(A) B = 90° - A
Known: b + B
a = b / tan(B) c = b / sin(B) A = 90° - B
Range of Values
Given the following parameters:
user_value:
min_value:
max_value:
actual_value: = if (user_value < min_value, min_value, if (user_value > max_value, max_value, user_value))
Specify a range of valid entries, with the min_value and max_value parameters; then, use the actual value if it is within the range; otherwise, use your minimum or maximum values.
Credits: Alfredo Medina, who posted this on March 23rd 2011
Circular Segments
To calculate the Segment length, the Chord Length, the Angle etc.
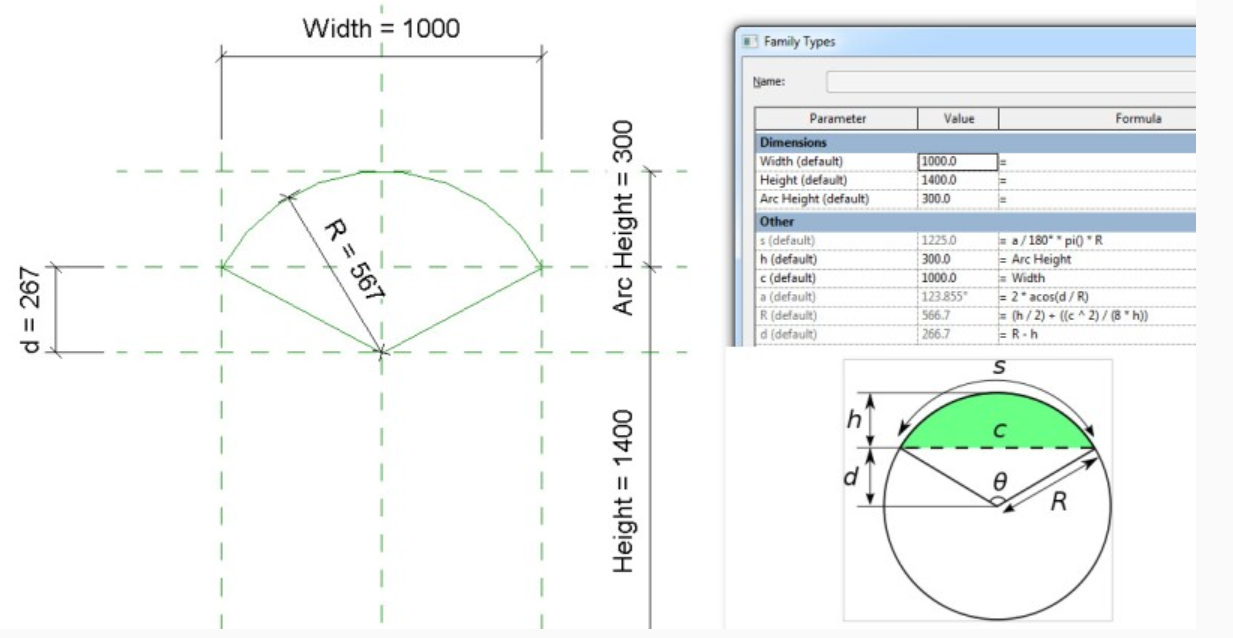
Sample file posted here
Inconsistent Units
There's a separate post explaining this behavior here: Revit - Inconsistent Units and how to neutralize them.
Round Function In Formulas
Values in formulas can be now rounded up or down. For example, when riser height is calculated, one needs the function “round” to find the appropriate value.
ROUND(x)
The round function returns a number rounded nearest to a whole number. It doesn’t take into consideration rounding direction (round up or down). If the number is (for example) from 24.5 to 24.9, the function rounds it to 25. If it is from 23.1 to 23.4, the function rounds it to 23.
Examples:
round ( 23.4) = 23
Round ( 23.5) = 24
Round ( 23.6) = 24
Round (-23.4) = -23
Round (-23.5) = -23
Round (-23.6) = -24
Syntax
The syntax for the round function is: round( number)
number is the number to round.
ROUNDDOWN(x)
“x” is a unitless value that should return the smallest integral value less than or equal to x.
For example:
rounddown ( 23.0) = 23
rounddown ( 23.5) = 23
rounddown ( 23.9) = 23
rounddown (-23.0) = -23
rounddown (-23.5) = -24
rounddown (-23.9) = -24
Syntax
The syntax for the rounddown function is: rounddown (number)
number is the number to round down.
ROUNDUP(x)
“x” is a unitless value that should return the largest integral value greater than or equal to x.
For example:
roundup ( 23.0) = 23
roundup ( 23.5) = 24
roundup ( 23.9) = 24
roundup (-23.0) = -23
roundup (-23.5) = -23
roundup (-23.9) = -23
Syntax
The syntax for the roundup function is: roundup (number) number is the number to round up. Note that when numbers such as 23.5 are rounded, they can result in either 23 or 24. To produce a stable result, for all the .5 cases, we round to the larger integer. That means that 23.5 is rounded to 24, while -23.5 to -23
Round to a number:
number to round: X
number to round to: Y
(ROUND(X/Y))*Y
rounding a parameter value to the nearest five would look like this:
(ROUND(<parameter>/5))*5

